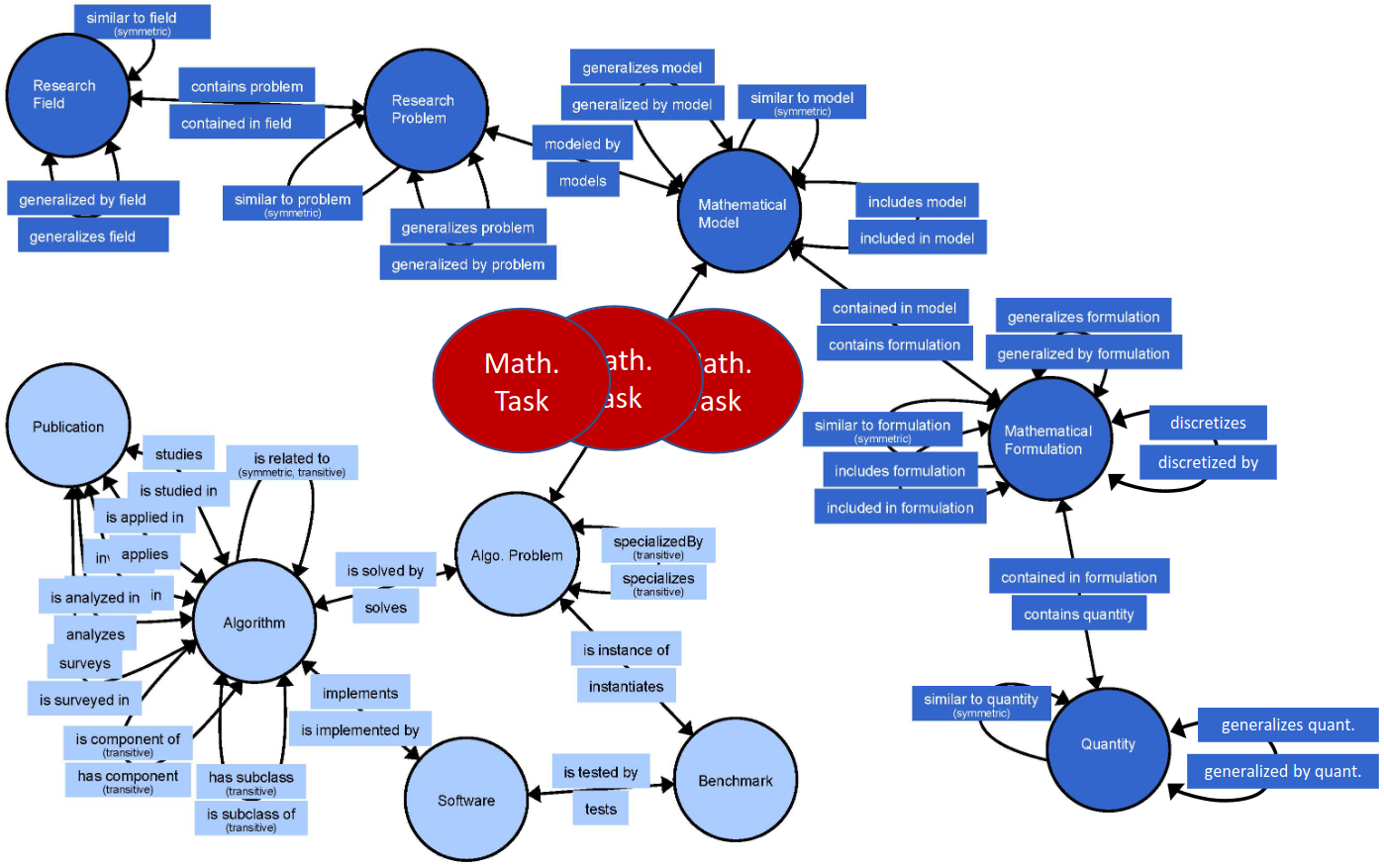
MathModDB

MathModDB is the database for mathematical models developed by MaRDIs TA4 as a knowledge graph. The ontology, which serves as the data model for the knowledge graph, encompasses seven classes (as of January 2024: "Research Field," "Research Problem," "Mathematical Model," "Mathematical Formulation," "Mathematical Task," "QuantityKind," and "Quantity.") It also captures the relationships between these classes, such as the association indicating that a model addresses a specific research problem. Furthermore, these entities are enriched with various attributes, including metadata like the mathematical formulations in LaTeX. This provides a thorough description of mathematical models and has been derived from the requirements stemming from the use case studies in M4.1. Initial datasets, exemplified by mathematical models such as Navier-Stokes (fluid dynamics), Michaelis-Menten (chemical kinetics), quantum dynamics (molecules and semiconductor devices), Line Planning, or Röntgen Transformation, have been seamlessly integrated into MathModDB.

In collaboration with Portal/TA2, the integration of MathModDB with MathAlgoDB was accomplished, underscoring the inherent connection between mathematical models and algorithms within the modeling-simulation workflow. This collaborative effort was showcased at various conferences, earning recognition with the Best Paper Award at MTSR 2023.

Models

Following models have been integrated into MathModDB:

TODO

Publications

Following publications with respect to MathModDB have been published

2023

Schembera, B., Wübbeling, F., Kleikamp, H., Biedinger, C., Fiedler, J., Reidelbach, M., Shehu, A., Schmidt, B., Koprucki, T., Iglezakis, D. and Göddeke, D., 2023. Ontologies for Models and Algorithms in Applied Mathematics and Related Disciplines. arXiv preprint arXiv:2310.20443.

Schembera, B., Riethmüller, C. and Göddeke, D., Enabling FAIR Data in Computational Science, Engineering and Mathematics through Knowledge Graphs.

Schembera, B., Wübbeling, F., Koprucki, T., Biedinger, C., Reidelbach, M., Schmidt, B., Göddeke, D. and Fiedler, J., 2023, September. Building Ontologies and Knowledge Graphs for Mathematics and its Applications. In Proceedings of the Conference on Research Data Infrastructure (Vol. 1). https://doi.org/10.52825/cordi.v1i.255